🔹 What is threadIdx.(x, y, z)?
Each thread in CUDA is part of a block. The thread has a position inside its block, described by threadIdx.x, threadIdx.y, and threadIdx.z.
🔸 Imagine a 3D block:
Let’s say we launch a block with dimensions (4, 3, 2):
- 4 threads in
x - 3 threads in
y - 2 threads in
z
Total threads per block: 4 × 3 × 2 = 24
Now, each thread can be uniquely identified by its (x, y, z) index inside that block:
threadIdx.z = 0 or 1
threadIdx.y = 0 to 2
threadIdx.x = 0 to 3
🔹 What is blockIdx.(x, y, z)?
A grid consists of many blocks. Each block has a position within the grid, described by blockIdx.x, blockIdx.y, and blockIdx.z.
🔸 Imagine a 2D grid of blocks:
Let’s say:
dim3 gridDim(3, 2); // 3 blocks in x, 2 in y
dim3 blockDim(4, 4); // 4×4 threads per block- So we have
3×2 = 6blocks total. - Each block is a 4×4 square of threads.
Combined Indexing
Each thread’s global position in the full grid is computed using both:
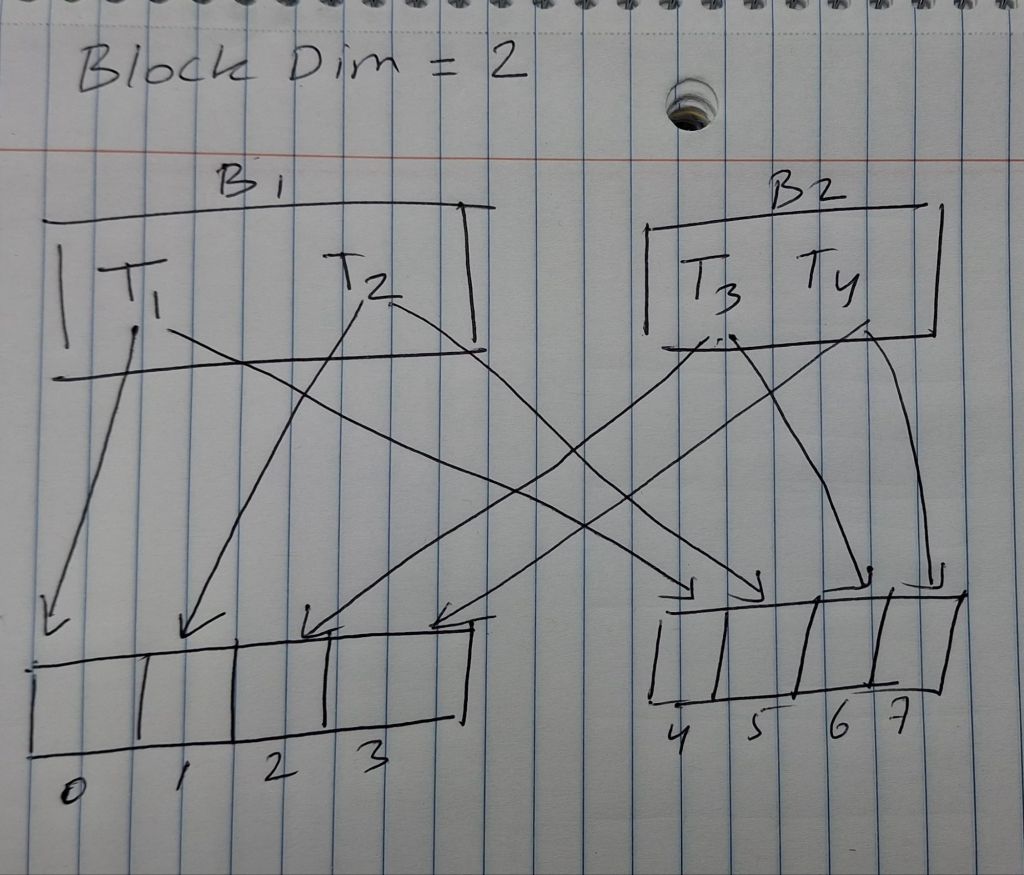
int global_x = blockIdx.x * blockDim.x + threadIdx.x;
int global_y = blockIdx.y * blockDim.y + threadIdx.y;
int global_z = blockIdx.z * blockDim.z + threadIdx.z;This maps the thread to a unique global position in the problem space (like pixels, matrix cells, etc).
Example:
#include <stdio.h>
__global__ void showThreadBlockIndex() {
printf("Block (%d, %d, %d), Thread (%d, %d, %d)\n",
blockIdx.x, blockIdx.y, blockIdx.z,
threadIdx.x, threadIdx.y, threadIdx.z);
}
int main() {
dim3 blockDim(2, 2, 1); // 2x2 threads per block
dim3 gridDim(3, 2, 1); // 3x2 blocks
showThreadBlockIndex<<<gridDim, blockDim>>>();
cudaDeviceSynchronize();
return 0;
}
Output:
Block (0,0,0), Thread (0,0,0)
Block (0,0,0), Thread (1,0,0)
Block (0,0,0), Thread (0,1,0)
Block (0,0,0), Thread (1,1,0)
Block (1,0,0), Thread (0,0,0)
...
🔷 Mapping Threads to Multidimensional Data
🟢 Easy
- What is the formula for computing a thread’s global row and column index in a 2D grid?
Answer:
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;🟡 Medium
- Convert a 2D index
(row, col)in a matrix of sizem × ninto a linear 1D index. Explain why this is needed in CUDA.
int index = row * n + col;🔴 Hard
- Write code that handles boundary conditions for a thread operating on a 62×76 image using a 16×16 block size. Only valid threads should modify image data.
#include <stdio.h>
#include <cuda_runtime.h>
// CUDA kernel to process a grayscale image
__global__ void processImage(unsigned char* image, int width, int height) {
int x = blockIdx.x * blockDim.x + threadIdx.x; // column
int y = blockIdx.y * blockDim.y + threadIdx.y; // row
if (x < width && y < height) {
int index = y * width + x;
image[index] = 255; // Example Operation: Set pixel to white
}
}
int main() {
const int width = 76;
const int height = 62;
const int imageSize = width * height;
// Host and device image pointers
unsigned char* image_h = (unsigned char*)malloc(imageSize);
unsigned char* image_d;
// Allocate memory on device
cudaMalloc(&image_d, imageSize * sizeof(unsigned char));
cudaMemset(image_d, 0, imageSize); // optional: initialize to black
// Launch CUDA kernel
dim3 blockDim(16, 16);
dim3 gridDim((width + blockDim.x - 1) / blockDim.x,
(height + blockDim.y - 1) / blockDim.y);
processImage<<<gridDim, blockDim>>>(image_d, width, height);
cudaDeviceSynchronize();
// Copy result back to host
cudaMemcpy(image_h, image_d, imageSize, cudaMemcpyDeviceToHost);
// Optional: print a few pixels
printf("First 10 pixels after kernel:\n");
for (int i = 0; i < 10; ++i) {
printf("Pixel %d = %d\n", i, image_h[i]);
}
// Free memory
cudaFree(image_d);
free(image_h);
return 0;
}
🔷 Image Blur – A More Complex Kernel
The following program takes in a RGB image in PGM file format and blurs it using 3×3 kernel average
#include <stdio.h>
#include <stdlib.h>
#include <cuda_runtime.h>
// ------------------------
// Utility to read PGM file
// ------------------------
unsigned char* readPGM(const char* filename, int* width, int* height) {
FILE* f = fopen(filename, "rb");
if (!f) { perror("File open failed"); exit(1); }
char magic[3];
fscanf(f, "%2s", magic);
if (magic[0] != 'P' || (magic[1] != '5' && magic[1] != '2')) {
fprintf(stderr, "Not a PGM file\n");
exit(1);
}
// Skip comments
int c;
do { c = fgetc(f); } while (c == '#');
ungetc(c, f);
fscanf(f, "%d %d\n", width, height);
int maxval;
fscanf(f, "%d\n", &maxval);
unsigned char* data = (unsigned char*)malloc((*width) * (*height));
fread(data, 1, (*width) * (*height), f);
fclose(f);
return data;
}
// ------------------------
// Utility to write PGM file
// ------------------------
void writePGM(const char* filename, unsigned char* data, int width, int height) {
FILE* f = fopen(filename, "wb");
fprintf(f, "P5\n%d %d\n255\n", width, height);
fwrite(data, 1, width * height, f);
fclose(f);
}
// ------------------------
// CUDA blur kernel (3x3 average)
// ------------------------
__global__ void blurKernel(unsigned char* input, unsigned char* output, int width, int height) {
int x = blockIdx.x * blockDim.x + threadIdx.x; // col
int y = blockIdx.y * blockDim.y + threadIdx.y; // row
if (x > 0 && x < width - 1 && y > 0 && y < height - 1) {
int sum = 0;
for (int dy = -1; dy <= 1; dy++) {
for (int dx = -1; dx <= 1; dx++) {
int nx = x + dx;
int ny = y + dy;
sum += input[ny * width + nx];
}
}
output[y * width + x] = sum / 9;
}
}
int main(int argc, char** argv) {
if (argc != 2) {
printf("Usage: ./blur_pgm image.pgm\n");
return 1;
}
int width, height;
unsigned char* image_h = readPGM(argv[1], &width, &height);
unsigned char* result_h = (unsigned char*)malloc(width * height);
unsigned char *image_d, *result_d;
cudaMalloc(&image_d, width * height);
cudaMalloc(&result_d, width * height);
cudaMemcpy(image_d, image_h, width * height, cudaMemcpyHostToDevice);
dim3 blockDim(16, 16);
dim3 gridDim((width + 15) / 16, (height + 15) / 16);
blurKernel<<<gridDim, blockDim>>>(image_d, result_d, width, height);
cudaDeviceSynchronize();
cudaMemcpy(result_h, result_d, width * height, cudaMemcpyDeviceToHost);
writePGM("blurred.pgm", result_h, width, height);
printf("Blurred image saved as 'blurred.pgm'\n");
// Cleanup
cudaFree(image_d);
cudaFree(result_d);
free(image_h);
free(result_h);
return 0;
}
In CUDA, blurring edges of an image is challenging because threads assigned to border pixels may attempt to access memory outside the valid image range. This can result in illegal memory access, crashes, or undefined behavior.
To avoid this, several strategies can be used:
- Boundary Checks
Each time a thread tries to access a neighbor pixel, it first checks whether the coordinates are within image bounds. For example, if (nx >= 0 && nx < width && ny >= 0 && ny < height), then it accesses the pixel; otherwise, it skips it. This method is simple and safe but may cause edge pixels to be averaged over fewer neighbors, leading to bias near the edges. - Clamp (Edge Replication)
This strategy keeps all neighbor accesses within valid bounds by clamping coordinates. For example, nx = min(max(x + dx, 0), width – 1). This causes edge pixels to use the closest valid border pixel, resulting in smoothed but slightly “smeared” edges. It’s commonly used in libraries like OpenCV. - Zero Padding
If a neighbor pixel is outside the image, it contributes a value of zero to the blur. This is safe but causes the image to darken around the edges since the average includes zeroes. - Mirror Padding
This reflects out-of-bound coordinates back into the image as if the image were mirrored at the border. For example, a coordinate -1 becomes 1, and width becomes width – 2. This method maintains edge structure but is more complex. - Ignore Borders
This is the simplest method. You only apply the blur to interior pixels (e.g., x > 0 && x < width – 1 && y > 0 && y < height – 1). Border pixels are left unchanged. This avoids all issues but leaves the border unprocessed.
Each method has trade-offs between safety, visual quality, and complexity. Clamp and mirror padding are the most visually pleasing, while boundary checks and ignoring borders are easiest to implement.
🔷 Matrix Multiplication
Matrix multiplication is a fundamental operation in scientific computing and deep learning. In CUDA, it involves mapping threads in a 2D grid to individual elements in the output matrix.
If matrix M is of size i × j, and N is j × k, then the result P is i × k, where:
Pseudocode:
for each row in M:
for each col in N:
P[row][col] = 0
for k from 0 to num_columns_in_M - 1:
P[row][col] += M[row][k] * N[k][col]
CUDA Code Sample:
float Pvalue = 0.0f;
for (int k = 0; k < common_dim; ++k) {
Pvalue += M[row * j + k] * N[k * k_dim + col];
}
P[row * k_dim + col] = Pvalue;Different difficulties of matrix multiplication cuda kernels:
1. Easy – Naive Kernel (One Thread Per Output Element)
//Each thread computes one P[row][col]. No optimizations.
__global__ void matMulNaive(float* A, float* B, float* C, int M, int N, int K) {
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
if (row < M && col < K) {
float sum = 0;
for (int i = 0; i < N; ++i) {
sum += A[row * N + i] * B[i * K + col];
}
C[row * K + col] = sum;
}
}2. Medium – Tiling with Shared Memory (Faster, Coalesced)
// Each block loads tiles of A and B into shared memory to reduce global memory // accesses.
__global__ void matMulTiled(float* A, float* B, float* C, int M, int N, int K) {
__shared__ float As[16][16];
__shared__ float Bs[16][16];
int tx = threadIdx.x;
int ty = threadIdx.y;
int row = blockIdx.y * 16 + ty;
int col = blockIdx.x * 16 + tx;
float sum = 0;
for (int t = 0; t < (N + 15) / 16; ++t) {
if (row < M && t * 16 + tx < N)
As[ty][tx] = A[row * N + t * 16 + tx];
else
As[ty][tx] = 0;
if (t * 16 + ty < N && col < K)
Bs[ty][tx] = B[(t * 16 + ty) * K + col];
else
Bs[ty][tx] = 0;
__syncthreads();
for (int k = 0; k < 16; ++k)
sum += As[ty][k] * Bs[k][tx];
__syncthreads();
}
if (row < M && col < K)
C[row * K + col] = sum;
}
- In matrix multiplication, what computation does each thread perform?
🟡 Medium
- For two matrices M (64×32) and N (32×128), how would you organize threads using a 2D block/grid configuration? Provide block and grid dimensions.
🔴 Hard
- Write CUDA pseudocode for matrix multiplication using 2D blocks. Include formulas for
row,col, and loop index for dot product.
🔷 Summary Concepts
🟢 Easy
- Why does CUDA limit thread and block dimensions to 3D?
🟡 Medium
- Explain how you could simulate a 4D dataset (e.g.,
(t, z, y, x)) using a 3D CUDA grid and manual flattening.
🔴 Hard
- Given a 5D dataset with shape
(batch, t, z, y, x), write formulas to compute the 1D flattened index from 5D coordinates and vice versa.